2.6-梯度下降优化算法

本小节主要围绕梯度下降优化算法，随机梯度下降 SGD，动量算法 Momentum，梯度加速算法 NAG，AdaGrad，AdaDelta，均方根反向传播 RMSProp，Adam展开介绍。

# 随机梯度下降 SGD

先回忆一下随机梯度下降的基本算法，便于和后面的各种算法比较。图 2.6.1 中的梯度搜索轨迹为示意图。

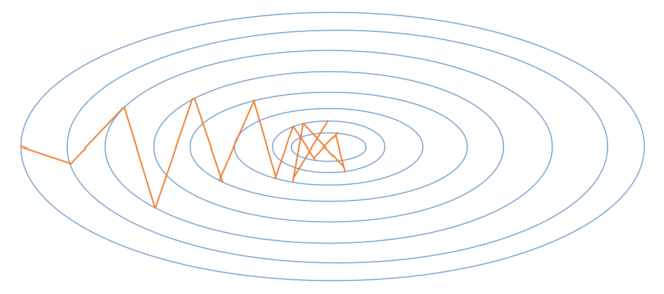
图 2.6.1 随机梯度下降算法的梯度搜索轨迹示意图

输入和参数

• $\eta$ - 全局学习率

算法

计算梯度：g​t​​=∇​θ​​J(θ​t−1​​) 更新参数：θ​t​​=θ​t−1​​−η⋅g​t​​

随机梯度下降算法，在当前点计算梯度，根据学习率前进到下一点。到中点附近时，由于样本误差或者学习率问题，会发生来回徘徊的现象，很可能会错过最优解。

# 动量算法 Momentum

SGD方法的一个缺点是其更新方向完全依赖于当前batch计算出的梯度，因而十分不稳定，因为数据有噪音。

Momentum算法借用了物理中的动量概念，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力。Momentum算法会观察历史梯度，若当前梯度的方向与历史梯度一致（表明当前样本不太可能为异常点），则会增强这个方向的梯度。若当前梯度与历史梯度方向不一致，则梯度会衰减。

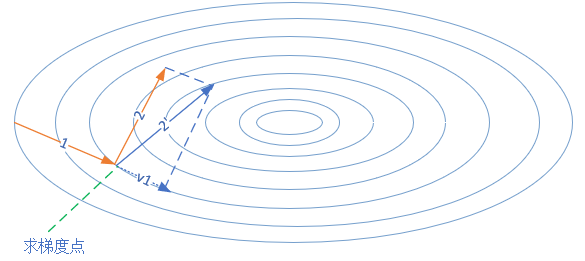
图 2.6.2 动量算法的前进方向

图 2.6.2 中，第一次的梯度更新完毕后，会记录v​1​​的动量值。在“求梯度点”进行第二次梯度检查时，得到2号方向，与v​1​​的动量组合后，最终的更新为2'方向。这样一来，由于有v​1​​的存在，会迫使梯度更新方向具备“惯性”，从而可以减小随机样本造成的震荡。

• 输入和参数

  • $\eta$ - 全局学习率
  • $\alpha$ - 动量参数，一般取值为0.5, 0.9, 0.99
  • v​t​​ - 当前时刻的动量，初值为0

• 算法

计算梯度：g​t​​=∇​θ​​J(θ​t−1​​) 计算速度更新：v​t​​=α⋅v​t−1​​+η⋅g​t​​ (公式1) 更新参数：θ​t​​=θ​t−1​​−v​t​​ (公式2)

# 梯度加速算法 NAG

其核心思想是：注意到 momentum 方法，如果只看 α⋅v​t−1​​ 项，那么当前的θ经过momentum的作用会变成 θ−α⋅v​t−1​​。既然我们已经知道了下一步的走向，我们不妨先走一步，到达新的位置”展望”未来，然后在新位置上求梯度, 而不是原始的位置。

所以，同Momentum相比，梯度不是根据当前位置θ计算出来的，而是在移动之后的位置θ−α⋅v​t−1​​计算梯度。理由是，既然已经确定会移动θ−α⋅v​t−1​​，那不如之前去看移动后的梯度。

图 2.6.3 是NAG的前进方向。

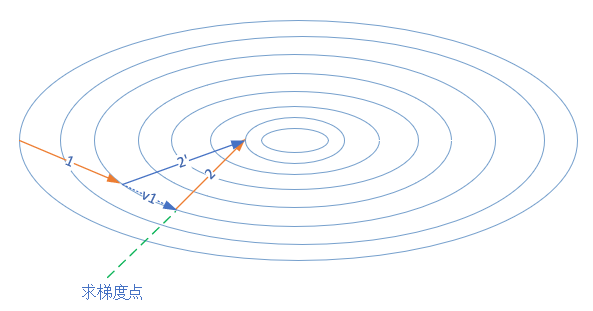
图 2.6.3 梯度加速算法的前进方向

这个改进的目的就是为了提前看到前方的梯度。如果前方的梯度和当前梯度目标一致，那我直接大步迈过去； 如果前方梯度同当前梯度不一致，那我就小心点更新。

输入和参数

• $\eta$ - 全局学习率
• $\alpha$ - 动量参数，缺省取值0.9
• $v$ - 动量，初始值为0

算法

临时更新：​θ​^​​=θ​t−1​​−α⋅v​t−1​​ 前向计算：f(​θ​^​​) 计算梯度：g​t​​=∇​​θ​^​​​​J(​θ​^​​) 计算速度更新：v​t​​=α⋅v​t−1​​+η⋅g​t​​ 更新参数：θ​t​​=θ​t−1​​−v​t​​

# AdaGrad

AdaGrad是一个基于梯度的优化算法，它的主要功能是：它对不同的参数调整学习率，具体而言，对低频出现的参数进行大的更新，对高频出现的参数进行小的更新。因此，他很适合于处理稀疏数据。

在这之前，我们对于所有的参数使用相同的学习率进行更新。但 Adagrad 则不然，对不同的训练迭代次数t，AdaGrad 对每个参数都有一个不同的学习率。这里开方、除法和乘法的运算都是按元素运算的。这些按元素运算使得目标函数自变量中每个元素都分别拥有自己的学习率。

输入和参数

• $\eta$ - 全局学习率
• $ϵ$ - 用于数值稳定的小常数，建议缺省值为1e-6
• $r=0$ 初始值

算法

计算梯度：g​t​​=∇​θ​​J(θ​t−1​​) 累计平方梯度：r​t​​=r​t−1​​+g​t​​⊙g​t​​ 计算梯度更新：Δθ=​ϵ+√​r​t​​​​​​​η​​⊙g​t​​ 更新参数：θ​t​​=θ​t−1​​−Δθ

# AdaDelta

Adaptive Learning Rate Method. ​[2]​​

AdaDelta法是AdaGrad 法的一个延伸，它旨在解决它学习率不断单调下降的问题。相比计算之前所有梯度值的平方和，AdaDelta法仅计算在一个大小为w的时间区间内梯度值的累积和。

但该方法并不会存储之前梯度的平方值，而是将梯度值累积值按如下的方式递归地定义：关于过去梯度值的衰减均值，当前时间的梯度均值是基于过去梯度均值和当前梯度值平方的加权平均，其中是类似上述动量项的权值。

• 输入和参数

  • $ϵ$ - 用于数值稳定的小常数，建议缺省值为1e-5
  • $\alpha \in [0,1)$ - 衰减速率，建议0.9
  • $s$ - 累积变量，初始值0
  • $r$ - 累积变量变化量，初始为0

• 算法

计算梯度：g​t​​=∇​θ​​J(θ​t−1​​) 累积平方梯度：s​t​​=α⋅s​t−1​​+(1−α)⋅g​t​​⊙g​t​​ 计算梯度更新：Δθ=√​​s​t​​+ϵ​​r​t−1​​+ϵ​​​​​⊙g​t​​ 更新梯度：θ​t​​=θ​t−1​​−Δθ 更新变化量：r=α⋅r​t−1​​+(1−α)⋅Δθ⊙Δθ

# 均方根反向传播 RMSProp

RMSprop 是由 Geoff Hinton 在他 Coursera 课程中提出的一种适应性学习率方法，至今仍未被公开发表。RMSprop法要解决AdaGrad的学习率缩减问题。

• 输入和参数

  • $\eta$ - 全局学习率，建议设置为0.001
  • $ϵ$ - 用于数值稳定的小常数，建议缺省值为1e-8
  • $\alpha$ - 衰减速率，建议缺省取值0.9
  • $r$ - 累积变量矩阵，与$\theta$尺寸相同，初始化为0

• 算法

计算梯度：g​t​​=∇​θ​​J(θ​t−1​​) 累计平方梯度：r=α⋅r+(1−α)(g​t​​⊙g​t​​) 计算梯度更新：Δθ=​√​r+ϵ​​​​​η​​⊙g​t​​ 更新参数：θ​t​​=θ​t−1​​−Δθ

# Adam - Adaptive Moment Estimation

计算每个参数的自适应学习率，相当于RMSProp + Momentum的效果，Adam​[4]​​算法在RMSProp算法基础上对小批量随机梯度也做了指数加权移动平均。和AdaGrad算法、RMSProp算法以及AdaDelta算法一样，目标函数自变量中每个元素都分别拥有自己的学习率。

• 输入和参数

  • $t$ - 当前迭代次数
  • $\eta$ - 全局学习率，建议缺省值为0.001
  • $ϵ$ - 用于数值稳定的小常数，建议缺省值为1e-8
  • β​1​​,β​2​​ - 矩估计的指数衰减速率，$\in [0,1)$，建议缺省值分别为0.9和0.999

• 算法

计算梯度：g​t​​=∇​θ​​J(θ​t−1​​) 计数器加一：$t=t+1$ 更新有偏一阶矩估计：m​t​​=β​1​​⋅m​t−1​​+(1−β​1​​)⋅g​t​​ 更新有偏二阶矩估计：v​t​​=β​2​​⋅v​t−1​​+(1−β​2​​)(g​t​​⊙g​t​​) 修正一阶矩的偏差：​m​^​​​t​​=m​t​​/(1−β​1​t​​) 修正二阶矩的偏差：​v​^​​​t​​=v​t​​/(1−β​2​t​​) 计算梯度更新：Δθ=η⋅​m​^​​​t​​/(ϵ+√​​v​^​​​t​​​​​) 更新参数：θ​t​​=θ​t−1​​−Δθ

# 小结与讨论

本小节主要介绍了梯度下降优化算法，随机梯度下降 SGD，动量算法 Momentum，梯度加速算法 NAG，AdaGrad，AdaDelta，均方根反向传播 RMSProp，Adam。

读者思考，如果当前的训练过程无法在单机单卡完成，需要扩展到多卡和多机分布式训练，如何实现以上训练算法？

# 参考文献

1. 《智能之门》，胡晓武等著，高等教育出版社

2. Duchi, J., Hazan, E., & Singer, Y. (2011). Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, 12(Jul), 2121-2159.

3. Zeiler, M. D. (2012). ADADELTA: an adaptive learning rate method. arXiv preprint arXiv:1212.5701.

4. Tieleman, T., & Hinton, G. (2012). Lecture 6.5-rmsprop: Divide the gradient by a running average of its recent magnitude. COURSERA: Neural networks for machine learning, 4(2), 26-31.

5. Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.

6. 周志华老师的西瓜书《机器学习》

7. Chawla N V, Bowyer K W, Hall L O, et al. SMOTE: synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16(1):321-357.

8. Inoue H. Data Augmentation by Pairing Samples for Images Classification[J]. 2018.

9. Zhang H, Cisse M, Dauphin Y N, et al. mixup: Beyond Empirical Risk Minimization[J]. 2017.

10. 《深度学习》- 伊恩·古德费洛

11. Shaoqing Ren, Kaiming He, Ross Girshick, and Jian Sun, Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks. Link: https://arxiv.org/pdf/1506.01497v3.pdf